Признаки сходимости несобственных интегралов. Примеры исследования несобственных интегралов на сходимость. Теорема сравнения несобственных интегралов

Несобственные интегралы первого рода. По сути это тот же определённый интеграл, но в случаях, когда интегралы имеют бесконечный верхний или нижний пределы интегрирования, или оба предела интегрирования бесконечны.

Несобственные интегралы второго рода. По сути это тот же определённый интеграл, но в случаях, когда интеграл берётся от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не имеет, обращаясь в бесконечность.

Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.

Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже - красного цвета), x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.

Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае - расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.

Несобственные интегралы первого рода - с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.

.

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.

Пример 1. Вычислить несобственный интеграл (если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.

В следующем примере подынтегральная функция почти как в примере 1, только степень икса - не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?

Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

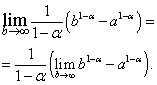
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .

В первом случае, то есть при имеет место . Если , то и не существует.

Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .

Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:

.

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл (если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

.

Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:

Несобственные интегралы второго рода - от неограниченных функций и их сходимость

Пусть функция f (x ) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.

Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.

.

Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае - расходящимся.

Используя формулу Ньютона-Лейбница, выводим.

Примеры исследования несобственных интегралов на сходимость

Пример 1
.

Таким образом, данный интеграл сходится при a>1 и расходится при a£1.

Пример 2 Исследовать на сходимость . Вычислим интеграл по определению:
.

Таким образом, данный интеграл сходится при a<1 и расходится при a³1.

Пример 3 Исследовать на сходимость .

<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два

.

Сходимость первого интеграла I1 исследуем с помощью эквивалентной функции: (т. к. n>0), а интеграл сходится при m>-1 (пример 2). Аналогично, для интеграла I2:

А интеграл сходится при m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 и m+n<-1, и будет расходится при нарушении хотя бы одного из них.

Пример 4 Исследовать на сходимость .

Подынтегральная функция может быть бесконечно большой (если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:

Так как arctgx »x при x®0, то интеграл I1 эквивалентен интегралу , который сходится при m+1>-1 т. е. при m>-2 (пример1).

Для подынтегральная функции в несобственном интеграле первого рода I2 подберем эквивалентную:

т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n<-1, и расходится в противном случае.

Объединяя условия сходимости интегралов I1 и I2 получим условия сходимости исходного интеграла: m>-2 и m+n<-1 одновременно.

Замечание. В примерах 2-4 использовался 2 признак сравнения, который обеспечивает необходимые и достаточные условия сходимости, что позволяет, установив сходимость при некотором условии на значения параметров, не доказывать расходимость интеграла при нарушении полученных условий сходимости.

Пример 5 Исследовать на сходимость .

Данный интеграл содержит особую точку 0, в которой подынтегральная функция может обращается в бесконечность при p<0, поэтому снова разобьем исходный интеграл на два:

.

Интеграл I1 является несобственным интегралом второго рода, и подынтегральная функция эквивалентна при x®0 функции xp (e-x ®1 при x®0), т. е. I1 сходится при p>-1 (пример 1).

Интеграл I2 является несобственным интегралом первого рода. Подобрать функцию, эквивалентную подынтегральной функции, такую, чтобы она не содержала показательной функции, не удается. Поэтому использовать признак сравнения 2, как в предыдущих примерах, нельзя. Применим первый признак сравнения, для чего используем следующий известный факт:

При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax < M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:

Т. е. интеграл I2 сходится при любом p.

Таким образом, исходный интеграл сходится при p>-1.

Пример 6 Исследовать на сходимость .

Проведем замену переменной: t = lnx, и получим

Разбиение интеграла на два произведено аналогично примеру 5. Интеграл I1 полностью эквивалентен интегралу I1 из примера 5 и, следовательно, сходится при q<1.

Рассмотрим интеграл I2 . При условии 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения и a=(1-p)/2.).

Итак, I2 сходится при p>1. Однако, на этом исследование сходимости этого интеграла не закончено, так как использованный признак сходимости дает только достаточные условия сходимости. Поэтому нужно исследование сходимости при 1-p£0.

Рассмотрим случай p=1. Тогда интеграл I2 эквивалентен , который сходится при q>1 (заметим, что в этом случае интеграл I1 расходится) и расходится в противном случае.

При p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что При 1-p>0, и, следовательно, начиная с некоторого А>1 выполнено T - Q E (1- P ) T ³ M=const>0. Тогда для интеграла I2 справедлива оценка

,

Где интеграл в правой части расходится, что и доказывает расходимость интеграла I2 .

Суммируя полученные результаты, получаем что исходный интеграл сходится при q<1 и p>1, в противном случае интеграл расходится.

Пример 6 Исследовать на абсолютную и условную сходимость .

Разобьем исходный интеграл на два:

.

Сходимость. Интеграл I1 эквивалентен , т. е. сходится при p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.

Интеграл I2 сходится про признаку Дирихле-Абеля при p>0 т. к. первообразная sin(x) ограничена, а функция 1/xp монотонно стремится к нулю при x стремящемся к бесконечности.

Покажем, что при p£0 интеграл расходится. Воспользуемся для этого критерием Коши, а точнее его отрицанием

.

Возьмем в качестве R1и R2 следующие величины: R1=2pk и R2=2pk+p/2, тогда

, при p>0.

Таким образом, интеграл сходится при 0

Абсолютная сходимость Абсолютная сходимость интеграла I1 уже установлена, рассмотрим абсолютную сходимость I2 . Оценим интеграл сверху:

, т. е. интеграл сходится при p>1.

Для доказательства расходимости при p£1 оценим интеграл снизу

.

Разобьем последний интеграл от разности функций на разность интегралов

.

Если оба интеграла сходятся, то и интеграл от разности сходится, если один из интегралов расходится, а другой сходится - то интеграл от разности расходится. В случае расходимости обоих интегралов сходимость интеграла от разности подлежит дальнейшему исследованию. Нас интересует второй из описанных случаев.

Расходится (пример 1) при p<1. сходится по признаку Дирихле-Абеля при 1>p>0 (см. Сходимость), следовательно интеграл оценивается снизу расходящимся интегралом, т. е. расходится.

Случай p³1 нас не интересует, т. к. при этих значениях параметра интеграл расходится.

Таким образом, исходный интеграл сходится абсолютно при 0

1. Несобственные интегралы с бесконечными пределами

Вспомним определение интеграла как предела интегральных сумм:

В определении предполагается, что интервал интегрирования конечен, а функция f (x) непрерывна в нем. Нарушение этих предположений приводит к несобственным интегралам.

Определение. Если интеграл стремится к конечному пределу при неограниченном возрастании “b” , то этот предел называют несобственным интегралом с бесконечной верхней границей от функции f (x) и обозначают символом

В этом случае говорят, что несобственный интеграл существует или сходится.

Если указанный предел не существует или существует, но бесконечен, то говорят, что интеграл не существует или расходится.

Аналогично определяется несобственный интеграл с бесконечной нижней границей:

Несобственный интеграл с двумя бесконечными границами определяется формулой:

где с - любая фиксированная точка на оси Ох.

Итак, несобственные интегралы могут быть с бесконечно нижней границей, с бесконечно верхней границей, а также с двумя бесконечными границами.

Признаки сходимости. Абсолютная и условная сходимость

Интеграл существует только тогда, когда существует каждый из интегралов: и .

Пример. Исследовать на сходимость интеграл

Полагая с = 0, получим:

т.е. интеграл сходится.

Иногда нет необходимости вычислять несобственный интеграл, а достаточно лишь знать, сходится он или расходится, сравнив его с другим интегралом.

Теорема сравнения несобственных интегралов.

Пусть в интервале функция f (x) имеет несколько (конечное число) точек разрыва первого рода, это “препятствие” легко устранить, разбив отрезок точками разрыва на несколько отрезков, вычислить определенные интегралы на каждом отдельном участке и результаты сложить.

Рассмотрим определенный интеграл от функции, неограниченной при приближении к одному из концов отрезка , например, .

(В таких случаях обычно говорят: ’’Функция имеет бесконечный разрыв на правом конце отрезка интегрирования’’.)

Ясно, что обычное определение интеграла здесь теряет свой смысл.

Определение . Несобственным интегралом от функции f(x), непрерывной при а £ х < b и неограниченной при x ® b - 0, называется предел:

Аналогично определяется несобственный интеграл от функции, имеющей бесконечный разрыв на левом конце отрезка:

Следовательно, на участке [ -1, 0] интеграл расходится.

Значит на участке интеграл также расходится.

Таким образом, данный интеграл расходится на всем отрезке [-1, 1]. Отметим, что если бы мы стали вычислять данный интеграл, не обращая внимания на разрыв подынтегральной функции в точке x = 0, то получили бы неверный результат. Действительно,

, что невозможно.

Итак, для исследования несобственного интеграла от разрывной функции, необходимо "разбить" его на несколько интегралов и исследовать их.